ਬਹੁਤ ਸਾਰੇ ਉਪਭੋਗਤਾ ਐਕਸਲ ਦੀ ਪੂਰੀ ਸ਼ਕਤੀ ਬਾਰੇ ਵੀ ਨਹੀਂ ਜਾਣਦੇ. ਖੈਰ, ਹਾਂ, ਅਸੀਂ ਸੁਣਿਆ ਹੈ ਕਿ ਟੇਬਲ ਦੇ ਨਾਲ ਕੰਮ ਕਰਨ ਦਾ ਪ੍ਰੋਗਰਾਮ, ਹਾਂ ਉਹ ਇਸ ਦੀ ਵਰਤੋਂ ਕਰਦੇ ਹਨ, ਉਹ ਕੁਝ ਦਸਤਾਵੇਜ਼ਾਂ ਨੂੰ ਵੇਖਦੇ ਹਨ. ਮੈਂ ਮੰਨਦਾ ਹਾਂ, ਮੈਂ ਇਕ ਸਮਾਨ ਉਪਯੋਗਕਰਤਾ ਸੀ, ਜਦੋਂ ਤਕ ਮੈਂ ਦੁਰਘਟਨਾ ਨਾਲ ਇਕ ਸਧਾਰਣ ਜਿਹੇ ਸਧਾਰਣ ਕੰਮ ਨੂੰ ਠੋਕਰ ਨਹੀਂ ਮਾਰਦਾ: ਐਕਸਲ ਵਿਚ ਮੇਰੀ ਇਕ ਟੇਬਲ ਵਿਚ ਸੈੱਲਾਂ ਦੇ ਜੋੜ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ. ਮੈਂ ਇਹ ਇੱਕ ਕੈਲਕੁਲੇਟਰ ਤੇ ਕਰਦਾ ਸੀ (ਹੁਣ ਹਾਸੋਹੀਣਾ :-P), ਪਰ ਇਸ ਵਾਰ ਟੇਬਲ ਬਹੁਤ ਵੱਡਾ ਸੀ, ਅਤੇ ਫੈਸਲਾ ਕੀਤਾ ਕਿ ਇਹ ਘੱਟੋ ਘੱਟ ਇੱਕ ਜਾਂ ਦੋ ਸਧਾਰਣ ਫਾਰਮੂਲੇ ਦਾ ਅਧਿਐਨ ਕਰਨ ਦਾ ਸਮਾਂ ਸੀ ...
ਇਸ ਲੇਖ ਵਿਚ ਮੈਂ ਜੋੜ ਫਾਰਮੂਲੇ ਬਾਰੇ ਗੱਲ ਕਰਾਂਗਾ ਇਸ ਨੂੰ ਸਮਝਣਾ ਸੌਖਾ ਬਣਾਉਣ ਲਈ, ਕੁਝ ਕੁ ਸਧਾਰਣ ਉਦਾਹਰਣਾਂ 'ਤੇ ਵਿਚਾਰ ਕਰੋ.
1) ਕਿਸੇ ਵੀ ਪ੍ਰਾਇਮਸ ਦੀ ਰਕਮ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ, ਤੁਸੀਂ ਐਕਸਲ ਦੇ ਕਿਸੇ ਵੀ ਸੈੱਲ ਤੇ ਕਲਿਕ ਕਰ ਸਕਦੇ ਹੋ ਅਤੇ ਇਸ ਵਿਚ ਲਿਖ ਸਕਦੇ ਹੋ, ਉਦਾਹਰਣ ਲਈ, "= 5 + 6", ਫਿਰ ਬਸ ਐਂਟਰ ਦਬਾਓ.
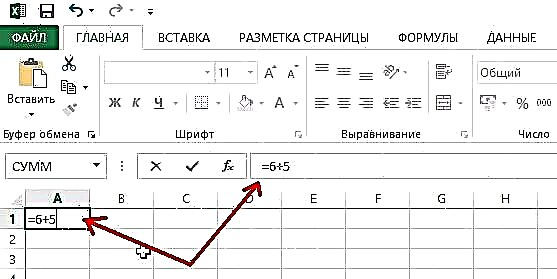
2) ਨਤੀਜਾ ਬਹੁਤਾ ਸਮਾਂ ਨਹੀਂ ਲੈਂਦਾ, ਜਿਸ ਸੈੱਲ ਵਿੱਚ ਤੁਸੀਂ ਫਾਰਮੂਲਾ ਲਿਖਿਆ ਸੀ ਨਤੀਜਾ "11" ਦਿਸਦਾ ਹੈ. ਤਰੀਕੇ ਨਾਲ, ਜੇ ਤੁਸੀਂ ਇਸ ਸੈੱਲ ਤੇ ਕਲਿਕ ਕਰੋ (ਜਿਥੇ ਨੰਬਰ 11 ਲਿਖਿਆ ਗਿਆ ਹੈ) - ਫਾਰਮੂਲਾ ਬਾਰ ਵਿੱਚ (ਉੱਪਰਲਾ ਸਕ੍ਰੀਨਸ਼ਾਟ ਵੇਖੋ, ਐਰੋ ਨੰਬਰ 2, ਸੱਜੇ ਪਾਸੇ) - ਤੁਸੀਂ 11 ਨੰਬਰ ਨਹੀਂ ਵੇਖ ਸਕੋਗੇ, ਪਰ ਸਾਰੇ ਇੱਕੋ ਜਿਹੇ ਹੋਣਗੇ "= 6 + 5".

3) ਹੁਣ ਸੈੱਲਾਂ ਤੋਂ ਸੰਖਿਆਵਾਂ ਦੇ ਜੋੜ ਦੀ ਗਣਨਾ ਕਰਨ ਦੀ ਕੋਸ਼ਿਸ਼ ਕਰੀਏ. ਅਜਿਹਾ ਕਰਨ ਲਈ, ਪਹਿਲਾ ਕਦਮ ਹੈ "ਫਾਰਮੂਲਾਸ" ਭਾਗ (ਉਪਰੋਕਤ ਮੀਨੂੰ) ਤੇ ਜਾਣਾ.
ਅੱਗੇ, ਕਈ ਸੈੱਲਾਂ ਦੀ ਚੋਣ ਕਰੋ ਜਿਨ੍ਹਾਂ ਦੇ ਮੁੱਲ ਦੀ ਰਕਮ ਜਿਸ ਦੀ ਤੁਸੀਂ ਗਣਨਾ ਕਰਨਾ ਚਾਹੁੰਦੇ ਹੋ (ਹੇਠਾਂ ਦਿੱਤੇ ਸਕ੍ਰੀਨ ਸ਼ਾਟ ਵਿੱਚ, ਲਾਭ ਦੇ ਤਿੰਨ ਕਿਸਮਾਂ ਹਰੀ ਵਿੱਚ ਉਭਾਰੇ ਗਏ ਹਨ). ਫਿਰ ਟੈਬ "ਆਟੋਸਮ" ਤੇ ਖੱਬਾ-ਕਲਿਕ ਕਰੋ.

4) ਨਤੀਜੇ ਵਜੋਂ, ਪਿਛਲੇ ਤਿੰਨ ਸੈੱਲਾਂ ਦਾ ਜੋੜ ਨੇੜੇ ਦੇ ਸੈੱਲ ਵਿੱਚ ਪ੍ਰਗਟ ਹੋਵੇਗਾ. ਹੇਠਾਂ ਸਕ੍ਰੀਨਸ਼ਾਟ ਵੇਖੋ.
ਤਰੀਕੇ ਨਾਲ, ਜੇ ਅਸੀਂ ਨਤੀਜੇ ਦੇ ਨਾਲ ਸੈੱਲ ਤੇ ਜਾਂਦੇ ਹਾਂ, ਤਾਂ ਅਸੀਂ ਆਪਣੇ ਆਪ ਫਾਰਮੂਲਾ ਵੇਖਾਂਗੇ: "= ਐਸਯੂਐਮ (ਸੀ 2: ਈ 2)", ਜਿੱਥੇ ਸੀ 2: ਈ 2 ਸੈੱਲਾਂ ਦਾ ਕ੍ਰਮ ਹੈ ਜਿਸ ਨੂੰ ਜੋੜਨ ਦੀ ਜ਼ਰੂਰਤ ਹੈ.

5) ਤਰੀਕੇ ਨਾਲ, ਜੇ ਤੁਸੀਂ ਸਾਰਣੀ ਵਿਚਲੀਆਂ ਬਾਕੀ ਸਾਰੀਆਂ ਕਤਾਰਾਂ ਵਿਚ ਜੋੜ ਦੀ ਗਣਨਾ ਕਰਨਾ ਚਾਹੁੰਦੇ ਹੋ, ਤਾਂ ਫਿਰ ਫਾਰਮੂਲਾ (= SUM (C2: E2)) ਨੂੰ ਦੂਜੇ ਸਾਰੇ ਸੈੱਲਾਂ ਵਿਚ ਕਾਪੀ ਕਰੋ. ਐਕਸਲ ਆਪਣੇ ਆਪ ਹਰ ਚੀਜ਼ ਦੀ ਗਣਨਾ ਕਰੇਗਾ.

ਇੱਥੋਂ ਤਕ ਕਿ ਅਜਿਹਾ ਜਾਪਦਾ ਸਧਾਰਣ ਫਾਰਮੂਲਾ - ਐਕਸਲ ਨੂੰ ਅੰਕੜੇ ਦੀ ਗਣਨਾ ਕਰਨ ਲਈ ਇਕ ਸ਼ਕਤੀਸ਼ਾਲੀ ਉਪਕਰਣ ਬਣਾਉਂਦਾ ਹੈ! ਹੁਣ ਕਲਪਨਾ ਕਰੋ ਕਿ ਐਕਸਲ ਇਕ ਨਹੀਂ, ਬਲਕਿ ਸੈਂਕੜੇ ਵੱਖ ਵੱਖ ਫਾਰਮੂਲੇ ਹਨ (ਵੈਸੇ, ਮੈਂ ਪਹਿਲਾਂ ਹੀ ਸਭ ਤੋਂ ਮਸ਼ਹੂਰ ਨਾਲ ਕੰਮ ਕਰਨ ਬਾਰੇ ਗੱਲ ਕੀਤੀ ਹੈ). ਉਹਨਾਂ ਦਾ ਧੰਨਵਾਦ, ਤੁਸੀਂ ਆਪਣਾ ਸਾਰਾ ਸਮਾਂ ਬਚਾਉਂਦੇ ਹੋਏ, ਕਿਸੇ ਵੀ ਚੀਜ਼ ਅਤੇ ਕਿਸੇ ਵੀ ਤਰੀਕੇ ਦੀ ਗਣਨਾ ਕਰ ਸਕਦੇ ਹੋ!
ਇਹ ਸਭ ਹੈ, ਸਾਰਿਆਂ ਨੂੰ ਚੰਗੀ ਕਿਸਮਤ.